The Geometry of Orbits:
Ellipses, Parabolas, and Hyperbolas
Orbits may have three distinct shapes
- Ellipses
- Closed orbits that have a period: eccentricity = 0 to 0.9999999. These are
the most common and interesting orbits because one object is 'captured' and
orbits another. Planet, minor planets, comets, and binar stars all have this
kind of orbit. The velocity in orbit is alway less than that needed to escape
from the central object.
- Hyperbolas
- Open orbits that do not close: eccentricity > 1. These orbits are
useful in describing two objects that pass by each other but are not
'captured' one by the other. They are used to explain the slingshot effect.
Velocities along the hyperbolic orbit are always greater than the escape
velocity.
- Parabolas
- Also an open orbit but a special boundary case with eccentricity = 1
(exactly). These orbits describe the case when an object falls in towards
another from very far away when they have very little velocity initially. Long
period comets have this type of orbit.
ELLIPTICAL ORBITS:
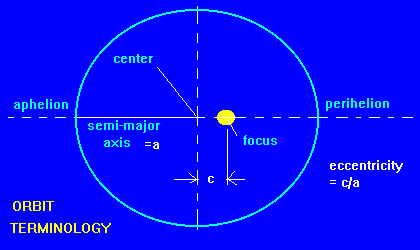 This diagram shows the parameters we need to talk about orbits.
This diagram shows the parameters we need to talk about orbits.
- The size is determined by the semi-major axis , a. (This is 1/2 of the
longes distance across the ellipse.
- The shape is determined by the eccentricity, e = c /a. c = the
displacement of the focus from the center of the ellipse.
- Two special points in the orbit (in this case orbit around the Sun)
- Perihelion: place in the orbit closest to the Sun
- Aphelion: place in the orbit farthest from the Sun
 This Diagram relates the various quantities using the unique
properties of ellipse.
This Diagram relates the various quantities using the unique
properties of ellipse.
- The relationship between a, b and c
- results from the fact that the length of a line drawn from one focus to
the ellipse then back to the other focus, will be equal to the major axis no
matter where on the ellipse you draw the line. The special case when that
point is at the end of the semi-minor axis is shown here and Pythagorean's
theorem gives the formula.
- The area
- of an ellipse is similar to that of a circle except instead of r*r it is
a*b. b can be written in terms of a and e.
- The length of the periheilion and aphelion
- is a result of the geometry along the major axis. Perihelion = a - c while
the aphelion = a + c
.
HYPERBOLIC ORBITS
 The hyperbola has two branches as shown in the diagram but
an orbit only uses one of them. There are relation between the dimensions of the
hyperbola in the same way as there is for the ellipse. As an object moves along
the hyperbolic orbit farther from the focus, it approaches the motion of a
straight line, asymptote line.
The hyperbola has two branches as shown in the diagram but
an orbit only uses one of them. There are relation between the dimensions of the
hyperbola in the same way as there is for the ellipse. As an object moves along
the hyperbolic orbit farther from the focus, it approaches the motion of a
straight line, asymptote line.
- Eccentricity = e = c/a (in this case it is greater than 1)
- The angle (delta) of the asymptote line is related to the eccentricity:
sin(delta) = a/c = 1/e
- The relationship c2 = a2 + b2 is
very similar to that for the ellipse. And in this case
b =
(e2 - 1)1/2 a
- Perihelion distance = rp = c - a = (e - 1) a
PARABOLIC ORBITS:
 A parbolic looks very similar to a hyperbola but there are no
asymptotic lines and there is only one branch. The parabola can be drawn by
locating points equal distant, d, from the line and the focus. The formula that
describes the shape of a parabola is called a quadratic and is in the
form
A parbolic looks very similar to a hyperbola but there are no
asymptotic lines and there is only one branch. The parabola can be drawn by
locating points equal distant, d, from the line and the focus. The formula that
describes the shape of a parabola is called a quadratic and is in the
form
y = rp + x2/4rp.
In the
figure to the right, y is measured to the left and x is measured upward.
rp = perihelion distance
The parameter, p = 2 rp in all parabolas.
Created: July , 1996,
Modified: 20 Feb, 2000
L.Bogan
 This diagram shows the parameters we need to talk about orbits.
This diagram shows the parameters we need to talk about orbits.
 This diagram shows the parameters we need to talk about orbits.
This diagram shows the parameters we need to talk about orbits.
 This Diagram relates the various quantities using the unique
properties of ellipse.
This Diagram relates the various quantities using the unique
properties of ellipse.
 The hyperbola has two branches as shown in the diagram but
an orbit only uses one of them. There are relation between the dimensions of the
hyperbola in the same way as there is for the ellipse. As an object moves along
the hyperbolic orbit farther from the focus, it approaches the motion of a
straight line, asymptote line.
The hyperbola has two branches as shown in the diagram but
an orbit only uses one of them. There are relation between the dimensions of the
hyperbola in the same way as there is for the ellipse. As an object moves along
the hyperbolic orbit farther from the focus, it approaches the motion of a
straight line, asymptote line. A parbolic looks very similar to a hyperbola but there are no
asymptotic lines and there is only one branch. The parabola can be drawn by
locating points equal distant, d, from the line and the focus. The formula that
describes the shape of a parabola is called a quadratic and is in the
form
A parbolic looks very similar to a hyperbola but there are no
asymptotic lines and there is only one branch. The parabola can be drawn by
locating points equal distant, d, from the line and the focus. The formula that
describes the shape of a parabola is called a quadratic and is in the
form